I love working in the IT industry. I can't think of any other industry that has had such a massive impact on the planet. I'm not just talking about technological progress. I'm talking about equity, opportunity, and progress. When I was growing up, I didn't have access to world-class information, resources, or people. There was really nobody to guide me on the things I wanted to achieve, and I didn't even know what I wanted to achieve because I couldn't see that far or where to look. You can imagine that things are pretty much the same today back home. For example, somebody in Silicon Valley has a much better opportunity of networking with people in the IT industry. Somebody in Washington DC can perhaps rub shoulders with politicians. Somebody from a wealthy family in New York is probably connected to the finance industry. All of them have a better chance than somebody who must walk 15 kilometers each way in a poor village in Africa to get fresh water. Your location matters; your circumstances still matter.
I'm not saying that the industry has solved this problem 100%. But I can argue that with the advent of things such as the Internet, and social networking, putting information and people together is so much more within reach than ever. And because of the pandemic and remote work being the norm, the world is flatter than ever before. It's to the extent that it has created a reverse problem: Information is no longer the issue; the deluge and quality of information is.
What does all this have to do with algorithms? Well, one of the things that I've heard over and over again in the IT business is that you don't need a CS degree to do well in this industry. And indeed, there are lots of examples of very successful people in our industry that have done well without a CS degree. Sadly, in the modern Google-driven development world, it's also becoming very evident that the quality of software has gone down. One of the key reasons for this is a change in focus to getting the task done without focusing on the fundamentals. This may get you to some distance, but it won't let you build world-class systems.
Ask anybody that's been around for a while. The concepts you see in service bus in Azure are the same concepts you see in MSMQ on premises, which are very similar to the concepts around window-messaging in Win32. The concepts around load balancing in the most complex systems are pretty much the same as sharding concepts in a modern distributed database or a complex global caching infrastructure, which are shockingly parallel to any other scenario where consistent hashing is applied.
I thought, therefore, it would be worth it to create a super back-to-basics article, which is language agnostic, and focuses on some basic algorithms that I wish everyone in the IT industry knew, whether or not they have a CS degree.
In this article, I'll go through these concepts one by one, and where applicable, I'll try to explain a practical application for these boring data structures and algorithms.
Array
An array is a data structure consisting of a collection of elements, each identified by an index or key. For example, let's say you want to store some numbers.
[1,5,7,0]
This could be an array. Think of how this would be represented in memory. You'd find a contiguous block of memory that could hold this array. You'd want to put some dimensions on how big of an object you can put in this array. Let's say you're dealing with integers. And you give yourself enough room that a 32-bit integer is the largest you need to deal with. For this array, you'd need a 32 bits-times-4 size of space. That's not so bad. But what if you wish to resize this array? Let's say you wish to add four more elements to the end. Now you have to find 8 x 32 bits of contiguous memory, and copy stuff around - assuming that the fifth 32-bit block after the fourth element was taken up. This is why, typically, in languages when we allocate arrays, we're forced to pick the size of it, so our program can allocate it and not have to keep hunting for space for it.
Another curious question you may be thinking: What if you need to stuff objects inside the array? Well, then you'd simply store locations (pointers) to where the actual object resides. In this case, the pointer would be 32-bits long. But aren't most computers 64-bit now? Should a pointer be 64-bits long, and how many programs would actually benefit from such a huge addressing space? A 64-bit address space can address 16-exabytes of memory. That is 17,179,869,184 gigabytes. The laptop I'm writing this on has 32 GB of RAM and it's more than enough for most of the programs I need. Should every array by default by 64-bit? Clearly, no. I'm oversimplifying here, but you get the idea.
Array List
As you can see, an array is quite useful, but having to pre-allocate what I may need ahead of time can be a real pain. In languages such as C++, you have methods such as calloc, malloc, and delete to play with memory. If you want 100% control of what your program is doing, that's indeed the way to go about it. But in the languages most people use (sorry C++), such as Java, C#, etc., we have higher level constructs to help us deal with managing memory in the shape of arrays. That concept is an array list. An array list is simply like an array, but you can dynamically increase its size as necessary. For instance, you can create an array list and it gives you four spaces. When you need to add a fifth element, the array list, implemented as a class, hunts for another four blocks somewhere, and manages all this for you. The number “4” is dependent on the framework. Some frameworks, such as .NET, allow you to instantiate an array list with a predefined initial capacity.
Additionally, an array list gives you convenient methods for stuff you'd usually do with an array, such as sort, BinarySearch, reverse etc. The code snippet below shows the usage of an ArrayList in C#. Java is quite similar.
ArrayList myAL = new ArrayList();
myAL.Add(1);
myAL.Add("Hello");
myAL.Add(new object());
Isn't an ArrayList wonderful? You no longer have to deal with malloc and friends. Umm, not so fast. There's no free ride here.
Behind the scenes, there's a bunch of magic going on, around allocating memory, juggling memory. You don't have to write that code, but you're paying the price for it. Additionally, because an ArrayList can hold heterogenous objects, such as the example above holds a string, a number, and an object, it won't offer you the best performance. Why would that be? Because storing every object requires special consideration. Pointers to objects behave differently than integers do. So you end up making worst-case assumptions, and you pay boxing and unboxing costs.
Most languages therefore offer generic implementations where you're required to pick a type during initialization, and that allows your program to allocate memory more effectively. In C#, this is the List<T> class, which you should almost always prefer over ArrayList. C++ had a very clever way of getting around this problem that was widely used in COM. It was the void** data type. It was a null pointer to a pointer, effectively letting you store anything without paying the additional memory cost. Still, the tradeoff there was that you had to be careful of what was on the other side of that void**, and it was easy to shoot yourself in the foot.
But let's admit it, arrays have one huge advantage. Once your array is set up, accessing any element via an indexer is fast.
Linked List
Arrays are useful, but they suffer from a pretty big disadvantage. As the array increases or decreases in size, you have to do all sorts of memory gymnastics. As you increase the size of the array, newer chunks of memory still need to be allocated. What happens when you delete stuff? Well, you're stuck with the poor choice of either leaving holes in your array, or moving stuff to the left once an element is deleted.
A linked list gets around these problems. It allows you to add elements as needed and delete elements without having to reshuffle your entire data structure. Here's how a linked list is represented in code (in C#).
public class Node {
public Node next;
public Object data;
}
public class LinkedList {
private Node head;
}
As you can see, a LinkedList is simply a placeholder that lets you hold the data you care about, and a pointer to where you can find the next element in this linked list. This looks like Figure 1.

Now you can grow this list on demand without having to allocate huge chunks of memory on the fly. For instance, if you were to add a fourth element, you'd simply update element 3's Next pointer to the location of the fourth element.
What happens if you wish to delete an element? For instance, what if I wish to delete element #2? Well, that's easy, you simply repoint element 1's next pointer to element 3. This is not computationally intensive.
What if you wanted to go backward in the linked list, i.e., find the parent of an element? You can simply add a “previous” pointer. This would be a doubly linked list.
So why don't we always use linked lists? Why do we even bother with arrays? The answer: Traversing a linked list is expensive. To get to element #5949, I have to go through 5948 elements first. But hey. At least I don't have to pay a huge up front and ongoing cost for allocating and managing all this memory.
Traversing a linked list is expensive.
Where would a linked list be useful? Think of any real-world representation of information. It's all about connections. I'm Sahil. I have a computer, a phone, a tablet. My phone has apps, memory, mail, photos. See? I am traversing a linked list. Actually, I'm traversing a graph, because the photos might be of my computer. More on this shortly.
Hash Table
I'm trying to store key value pairs. For instance, I have (person name, age) as a possible data structure I wish to store. Or maybe I want to store (identifier, person object) as a key value pair. So given an identifier, I want to quickly retrieve the person object.
Well, that's where a hash table fits. Much to my chagrin, it wasn't a table from Amsterdam. Let's first define what a hash is. A hash is a function that you pass into an object and it reliably, for the same object, gives you the same hash every time. Given that, if I were to pick a hash function and pass in an identifier, it would yield me a number where I can store a pointer to the person object.
For example, an identifier of “8ca0f7cb-cc5b-4c5d-b455-9e22681fe3b3” could perhaps resolve to a hash value of 95, and on location #95, I can store a pointer to the person object, as shown in Figure 2.
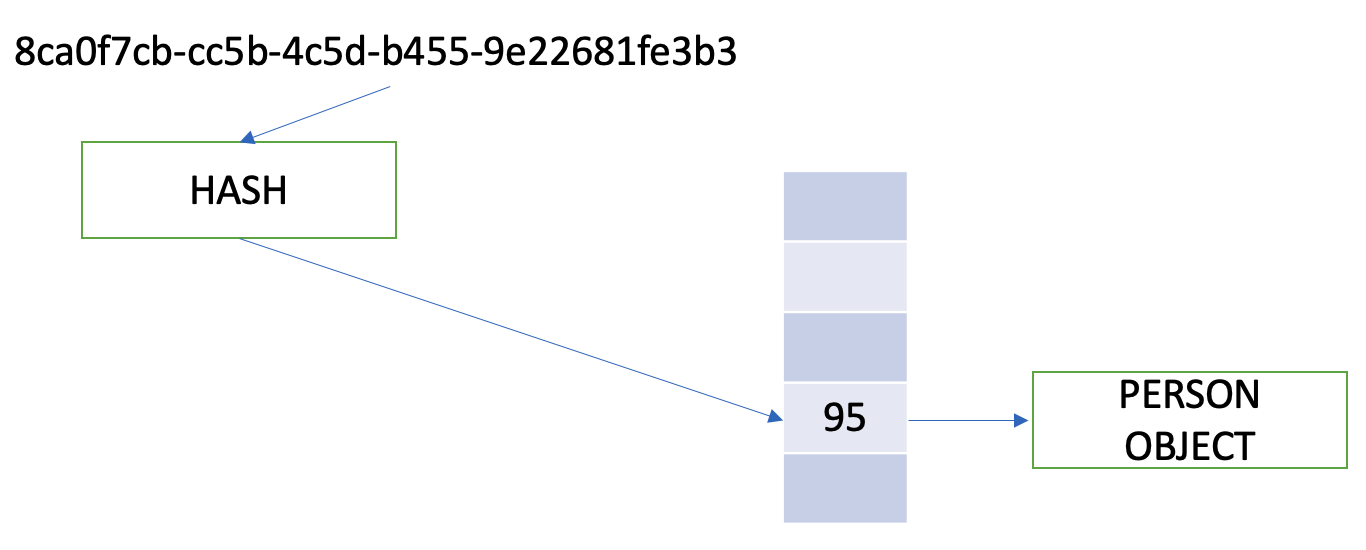
Problem solved, right? Nope. The problem is, the inputs are seemingly infinite, but the output of the hash function space is finite. So, you're bound to have collisions. There are various strategies to this problem. You could start storing linked lists at individual locations. Or you could use other structures, such as finding an empty bucket closest to the already filled location, or you could have a separate hash on top of a hash to increase the address space.
But either way, in a very large set of data, one advantage is clear: speed. If the number of entries can be roughly predicted and allocated for, you can pick just the right hash function that's the right balance of space and performance, and create a really fast lookup. The disadvantage, of course, is that every object is seemingly random. For instance, you may want to traverse through the objects and where your previous pick could effectively limit your address space, you gain no advantage by using a hash table. For example, I wish to represent all cars. But what if I want to narrow down to Toyota, and then Corolla. The fact that I've picked Toyota should help me speed up my lookup for Corolla. But in a hashtable, all elements are equally fast, or equally slow. And picking a poor hash function can really slow you down.
Now, you may be thinking, why does this all this even matter? Imagine that you're writing a cloud scale system, and every optimization translates to millions of dollars saved - suddenly, all this matters. But let's pick a more mundane example. You're writing a globally distributed system and you need a cache. Caches could be implemented as hashtables and you want to pick the right algorithm to avoid naming collisions or the appropriate data structures to speed up your lookups. What if one of your tasks was the search through your data? For example, you're implementing an autocomplete-like functionality. If I type “car,” I want card, carpet, and carry to be matched. I could do this using a hashtable, but would that be the best approach? Hashtables are great when I want consistent or almost consistent performance for each element. It's important to find the right tool for the right job.
Trees
Okay, so hashtables are very useful. But every element is equal to every other element. I wish I had a mechanism to bake some intelligence into my data. For instance, let's say that frequently I need to perform calculations against my data. I have a bunch of invoices, and I wish to easily sort them. Or I want to find the min/max of them. Or do stuff like find the average of all invoices less than $500. Are you aware of a program that lets you do this kind of magic? Of course. Excel does this. All the time.
I have no idea how Excel has been implemented behind the scenes. But I hope in a system optimized for traversing data, you'd use a structure such as trees.
For a moment, glance at the linked list data structure as shown in Figure 1. A tree is quite similar, except, in a linked list, you can link to only one other node. In a tree, you can link to multiple other nodes. A binary tree can link to exactly two other nodes. Also, a tree cannot be a loop. This means that element 1 cannot point to element 2 and then to 3, and 3 point back to 1.
Figure 3 shows a binary search tree. As you can see, every element has two possible children. The smaller is on the left, the larger is on the right. One or both elements can be null.
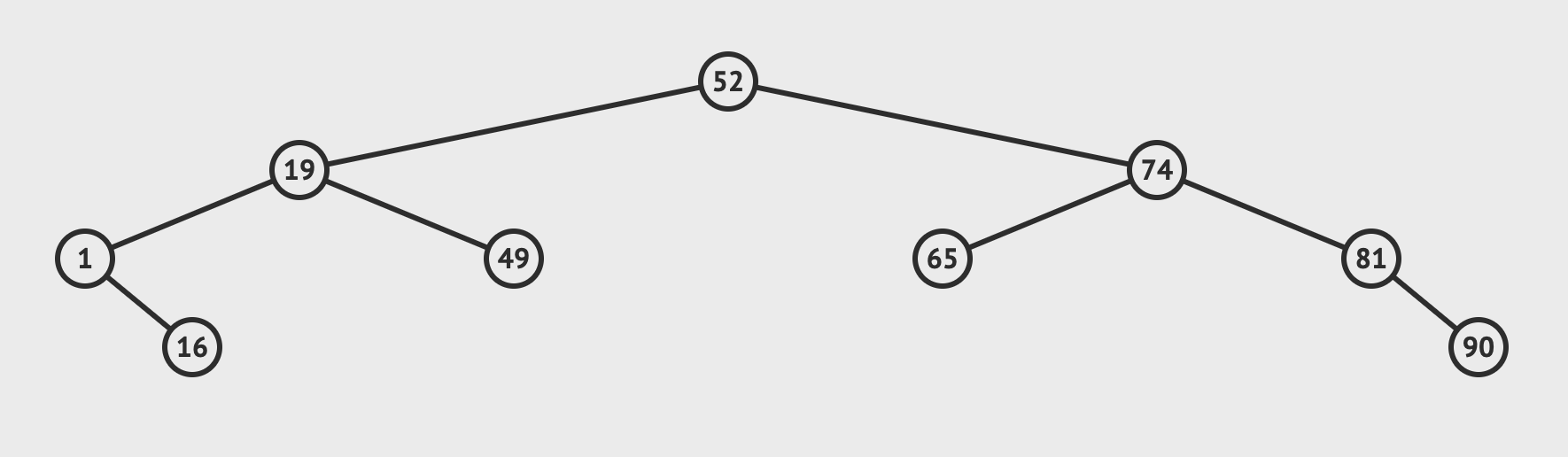
Now, if I gave you a problem, let's say: Find element #49. This problem in a hash table would be computationally expensive. You'd have the run the hash function for 49 (and assume 49 was a big complex object, such as an invoice). Then find the location, deal with collisions, and eventually land on the object and pass it back. What if I made the problem a little more complex: Find me the sum of all invoices less than 52. This would be very expensive in a hashtable.
Let's see how this works in a tree. To find element #49 (assuming it exists), I simply evaluate 49 < 52, and go left. The next element I arrive at is 19. Because 49 > 19, I go right and find what I'm looking for.
How would I do a sum? I'd use recursion or dynamic programming. This makes my job so much simpler. Even better, the amount of time it would take to compute any such problem will also become quite predictable.
Tries
A trie is a specific kind of a tree and it works great with strings. Imagine if you're building the spell check feature in MS Word. You want the feedback to the user to be fast and fluid. Let's say the user types “monkr”. This is clearly a spelling mistake. Let's think through the logic here.
First the user types “m”. Well, there are plenty of words that start with m. This is not a spelling mistake.
Then the user types “mo”. The user may be typing money, most, Monday, monkey, moo, mom. Again, not a spelling mistake so far.
Now the user types, mon. Still, this could be Monday, money, moniker, etc.
Finally, the user types “monk.” This is a word. But it could be the prefix for monkey, or monkfish, or monks.
Finally, the user types “monkr” - and we know for sure that this is a spelling mistake.
One thing is clear: at the type of every keystroke, you wish to very quickly evaluate whether or not this is leading to a real word or not. I guess I could have a huge look-up of words, such as a dictionary or a hash table. Every time the user types something, I could search. This is why my MacBook fan runs so fast. My MacBook Pro literally is MacBook hot air. Developers write poor code. I wish I had a data structure like that shown in Figure 4.
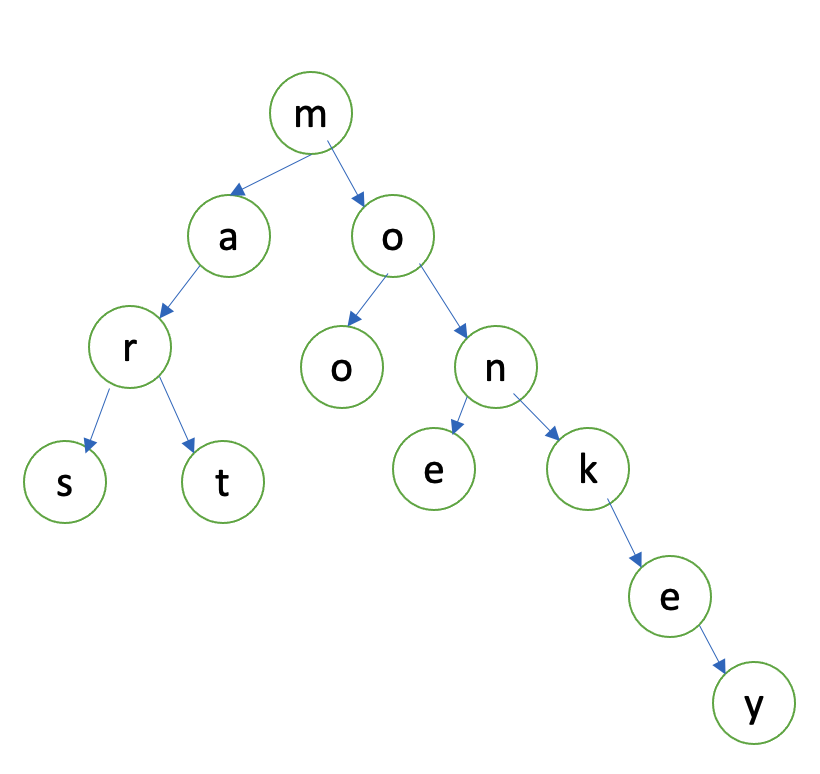
This kind of structure makes my job so much easier. Now when the user types in “m,” I quickly look up the “m” node and pass it back to the application. The next time I receive a key stroke, I expect the application to pass me the node it was working with. So I can quickly look at the children of “m” and easily evaluate “a” and “o” as valid children, but perhaps not “mt” as a valid word combination. The moment I run into an invalid word combination, i.e., no child found, I can show a red squiggly.
Imagine how useful this would be on a cellphone. What if you had approximate matching algorithms? For instance, that touch-type thing on your iPhone can look for word proximity to improve your typing. If you type “m” followed by “r” but you could then expand to the characters immediately around “r” as a possible mistype, “e,” “d,” “f,” “g,” and “t,” you can very quickly do a lookup in your trie, and immediately know that the user meant “me.” You can pair this with even more intelligence by adding probabilistic words and grammatical intelligence. Imagine how cumbersome it would be to write on a touch screen without all this?
It wasn't long ago that we had to deal with all these typos. In fact, in 2008, I remember using a Windows CE phone that had a stylus, and it had none of this intelligence built into it. It took an hour to compose an email. What boggles my mind is that we haven't brought all this intelligence to desktop programs, such as word processing applications, or rebooting IntelliSense to AI IntelliSense in Visual Studio. One can dream. Sigh! But have you noticed recently that some email applications have started making use of this? As you compose an email, they prompt you to fill a sentence. A huge time saver, and really hides my poor grammar too.
Graphs
Find me a word as overused as “graph” in our industry. No, I'm not talking about MSGraph or GraphQL, etc. This is a nonlinear data structure called “graph.” A graph, like a tree, is a collection of objects, called nodes or vertices.
The big difference between a tree and graph is that in a tree, the rules are a bit more rigid. Specifically with n nodes, you must have exactly n-1 edges, one edge for each parent-child relationship. Each node has exactly one parent. All nodes are reachable from the root and you can always traverse to the parent from any node.
In a graph, it's a bit more freeform. You have a bunch of nodes and a bunch of edges, and you connect them as you wish. Think of it this way: A tree is a specific kind of a graph.
Now this is getting interesting. Isn't information in the real world much more like a graph? Think of streets on a map. They all connect to each other - not like a tree, but more like a mesh, or, what's the word I'm looking for? A graph! What about cooking recipes? Imagine how boring life would be if you always had to think of recipe as a tree.
If you must have your pudding, you must finish your meat, so how can you have your pudding if you don't finish your meat? <g>
Boy, have we heard that before. Real world is much more colorful, and experimental. Graphs represent a much more natural way of information we see and need to represent in our data structures. And you can do all sorts of interesting things, such as adding weights to the edges - imagine how useful that would be when calculating the shortest driving distance between two points on a map. Or how about routing data between servers on the World Wide Web?
Now, how would you go about searching in this graph? For instance, calculating driving directions? This becomes a simple recursive function, where you can ask each child, “hey, do you have a path to such and such,” and you keep going until you reach that node. But this would be computationally expensive, you'd have to worry about loops, etc. So you can just do a breadth first search, where you ask all your children if they have a path until such and such node. And then keep storing the results in a stack until you get there.
And for the most commonly requested driving directions, you could pre-cache the results. You could also have varying weights on the edges, like one for speed and one for environmental impact. So you could do cool stuff like, “find me driving directions with the least environmental impact.”
Stacks and Queues
Stacks are exactly what they sound like - like a stack of plates but for data. Think of a data structure where you can add items one on top of another. If you wish to remove an item from a stack, you pop an item and the last inserted item is popped off. If you want to add an item, you push an item into the stack - akin to setting a plate on top of the stack.
Now you may wonder where this data structure is actually used. Well, this is used all the time, like when you call a function from another function. When you go from one function to another function, the state of the calling function must be preserved. All the variables of that function are pushed into the stack. When you return, everything can be popped off the stack.
It's useful, in fact, in any backtracking kind of application where, say, you're traversing a graph, and you want to back track your steps. Imagine you did a Google map search and you have driving directions. Now you wish to go step by step and decide to revert back from step 6 back to 5,4,3,2,1. This is an example of a stack.
Queues, on the other hand, are slightly different. Queues are first in, first out. Just like you'd imagine in real-world queues, the person who stands in the queue first gets served first. Queues are incredibly useful in real life. For example, let's say you're creating an ecommerce website. You quickly want to accept all orders as fast as you can while offering the user a very good user interface. Processing the order may take some time. You wish to accept the order and then put the fact that the order has been accepted and the details of the order into a queue. Now, a worker process, or more than one worker process, can start dequeuing orders from that queue in a first in, first out basis.
Expand this a little bit further. The message sent on that queue can have specific characteristics. Those characteristics may define the appropriate recipient or recipients for that message. For example, you can tap into the queue for logging purposes. Or you could say that “this kind of order” shall be processed by “that kind of worker.”
You can even offer transactional semantics on a queue. For instance, when you receive an order, you want to make sure that that order is processed. This means that when a worker dequeues a particular message, you want to make sure that their order is fulfilled. Instead of dequeuing a message, the worker can simply lock that message with a timestamp. The worker is required to renew their lock for a given time span. If the lock isn't renewed, you assume that the worker crashed. If the worker is still working on a particular order, the worker simply extends their lease. Essentially, this gives you some confidence that no messages are lost and they're all appropriately processed.
Summary
This article was extra fun. Usually whenever you're learning a concept, you're trying to solve a problem. Almost always, you're learning about some concept offered by Azure or AWS. Or maybe you're programming against an SDK, such as the .NET Framework. Someone else has done a lot of the thinking for us.
There's nothing wrong in targeting and thinking at that level. But if that's all you do, you're bound to make mistakes. It's akin to learning how to drive a car but knowing nothing about how the engine operates. How would you know, when your car is making a funny sound, that you're not driving with the parking brake on?
Yes, we all have such a friend, don't we? I hope in the programming world, this brief introduction to some of the common algorithms and data structures piqued your curiosity about an entire underworld that you want to know about.
I hope you found this article fun, and I hope to show you many other such practical applications in future articles.






